|
Estamos
interessados em detalhar um pouco mais o que acontece com a radiação
eletromagnética quando incide num meio com índice de
refração diferente daquela na qual ela se propaga. Em
particular queremos analisar os ângulos de reflexão e
refração e as amplitudes dos campos elétricos
transmitido e refletido.

Considere
dois meios homogêneos isotró-picos, lineares e não
condutores (s=J=0) com índices de
refração n1 e n2, separados por
uma interface localizada sobre o plano xz. Um raio de amplitude E,
propagando-se no meio 1 incide sobre a interface, formando um ângulo
q com o eixo y. O raio refletido tem amplitude
E' e sua direção de propagação é
especificada pelos ângulos q' e f'.
Analogamente, o raio refratado é especificado por E", q" e
f", como mostra a Fig. 6.12. Note o fato
de estarmos supondo que os três raios não estão
num mesmo plano.
Das equações de Maxwell podemos deduzir condições
de contorno que estabelecem a continuidade das componentes de e ao
se passar de um meio para outro. Os campos 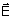 , ,
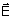 '
e '
e 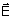 ''
são dados por: ''
são dados por:
enquanto
que os campos magnéticos se relacionam com os campos elétricos
através de:
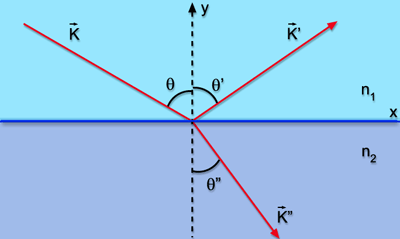
Fig. 6.12 - Geometria da reflexão
e refração de um raio de luz.
Tomando
um pequeno elemento de volume S dh contendo parte da interface (Fig.
6.13), podemos aplicar a forma integral da lei de Gauss:
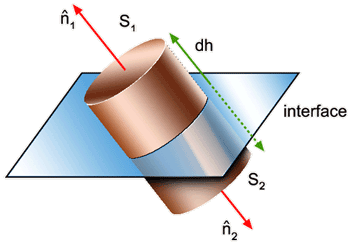
Fig. 6.13 - Elemento de volume usado na obtenção das
condições de contorno.
Como
a carga superficial é dada por
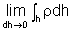 ,
ficamos com: ,
ficamos com:
Assim,
de acordo com a Fig. 6.13, temos:
Note
que S1 = S2 = S pois dh
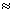 0 e
0 e
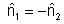 =
=
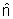 .
Logo, a equação acima nos leva a: .
Logo, a equação acima nos leva a:
que
estabelece que a variação da componente normal do deslocamento
elétrico é igual à carga superficial. No nosso
caso específico = 0, logo, a componente normal de
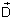 é contínua:
é contínua:
Procedendo
de maneira análoga com as outras equações de
Maxwell, obtemos:
A
eq. (6.17) nos diz que para y = 0 a componente tangencial do campo
elétrico é contínua, logo:
para
a componente x e
para
a componente z. Como estas igualdades são válidas para
qualquer t e qualquer ponto r da interface, devemos ter:
onde
 .
Esta última igualdade nos diz que os vetores .
Esta última igualdade nos diz que os vetores
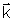 , ,
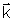 '
e '
e
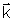 ''
são coplanares, isto é, f' = f" = 0 e portanto: ''
são coplanares, isto é, f' = f" = 0 e portanto:
Por
outro lado, k = k' pois k = w/v1 e k' = w'/v1 = w/v1. Logo, q = q', ou seja, o ângulo de incidência é
igual ao ângulo de reflexão q'.
O ângulo de refração q"
pode ser encontrado usando-se k = n1k0 e k"= n2k0 na eq. (6.22). Assim, n1sen
= n2sen , que é chamada de
lei de Snell.
Em resumo temos as seguintes regras: (i) os raios incidente, refletido
e refratado são coplanares, (ii) o ângulo de incidência
é igual ao ângulo de reflexão ?', e (iii) os ângulos
de incidência e refração se relacionam através
da lei de Snell
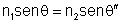 . .

Vamos
analisar dois casos: a) aquele em que é paralelo à interface
(e, portanto, perpendicular ao plano xy) como mostrado na Fig. 6.14(a),
e leva o nome TE (transversa elétrica) ou polarização
s (ou s) e (b) quando for paralelo à
interface, que corresponde à onda TM (transversa magnética)
também chamada polarização p
(ou p), mostrada na Fig. 6. 6.14(b). No caso (a)
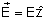 e para (b)
e para (b)
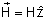 ,
o mesmo se dando com as ondas refletida e refratada. ,
o mesmo se dando com as ondas refletida e refratada.
Fig. 6.14 - Reflexão e refração de uma onda
(a)
TE (polarização s) e (b) TM (polarização
p).
Logo,
usando as eq. (6.17) e (6.19) podemos fazer a seguinte análise:
caso
a) TE
Usando
a eq. (6.11) para eliminar H em função de E, obtemos:
definidos
por:
Caso b) TM
Novamente, usando a eq. (6.11) para eliminar H em função
de E, obtemos:
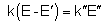 ,
de onde sai: ,
de onde sai:
As
equações acima podem ser modificadas usando-se a lei
de Snell
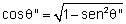 =
=
 ,
e o índice de refração relativo (n = n2/n1): ,
e o índice de refração relativo (n = n2/n1):
A Fig. 6.15 mostra a variação do coeficiente de reflexão
em função do ângulo de incidência quando
n2 > n1 (reflexão externa). O sinal negativo de significa
que o campo elétrico muda a fase em 1800
após a reflexão. Note que rp = 0 quando:
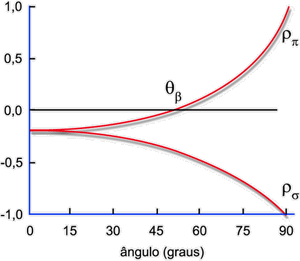
Fig. 6.15 - Coeficiente de reflexão externa.
Como n2 > n1 temos tgqB
> 1 e, consequentemente, qB > 45 . qB é conhecido com ângulo
de Brewster.
A Fig. 6.16 mostra o caso da reflexão interna (n1 > n2) com o ângulo
de Brewster, sendo agora menor que 450. Por outro lado, quando n = senq temos um ângulo crítico
qc acima do qual rs = rp = 1. Para n menor que
senq temos:
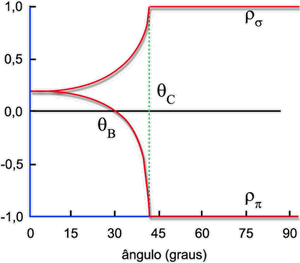
Fig. 6.16 - Coeficiente de reflexão interna.
Um
conceito erroneamente empregado é que se a refletividade é
unitária, nenhuma luz penetra no meio menos denso. Isto não
é verdade, como veremos a seguir. Supondo que a onda incidente
na interface é plana e tomando o campo elétrico na forma
exponencial, podemos escrever:
onde
na última passagem usamos o fato que ao onda se propaga no
plano xy (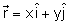 ).
Note que kx = k senq
e ky = k cosq
são as projeções de ).
Note que kx = k senq
e ky = k cosq
são as projeções de
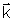 no plano xy. O módulo de k" é (w/c) n1. No meio com índice
n2, o campo elétrico pode
ser escrito de maneira similar: no plano xy. O módulo de k" é (w/c) n1. No meio com índice
n2, o campo elétrico pode
ser escrito de maneira similar:
sendo
as projeções de
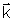 " dadas por kx" = k" senq"
e ky" = k" cosq",
e seu módulo por k"= (w/c)n2.
Lembrando que n = n2/n1, pela lei de Snell temos senq = n senq" e consequentemente: " dadas por kx" = k" senq"
e ky" = k" cosq",
e seu módulo por k"= (w/c)n2.
Lembrando que n = n2/n1, pela lei de Snell temos senq = n senq" e consequentemente:
Desta
forma, a parte espacial da fase da onda dada pela eq. (3.16) fica:
Como i2 = -1, o campo é dado por:
onde
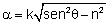 .
Note que a luz se propaga paralelamente à interface, na direção
do eixo x. Por outro lado, penetra no meio menos denso, porém
decaindo de forma exponencial. Em geral, a profundidade de penetração
é da ordem do comprimento de onda da luz. Pictoricamente, é
como se houvesse uma rampa na qual uma partícula (fóton)
sobe um pouco mas depois volta. Este processo na óptica leva
o nome de penetração em barreira ou tunelamento fotônico.
Isto fica mais claro se colocarmos dois prismas próximos, separados
por uma distância da ordem do comprimento de onda da luz, como
representado na Fig. 6.17. Desprezando as reflexões de Fresnel
nas faces de entrada e saida dos prismas, vemos que a intensidade
da luz transmitida decai exponencialmente com a separação
entre os prismas, de acordo com IT
= I0 exp (-ad).
No interior de cada prima o campo elétrico oscila harmonicamente
na direção y, mas entre eles decai exponencialmente
como mostrado na Fig. 6.17. .
Note que a luz se propaga paralelamente à interface, na direção
do eixo x. Por outro lado, penetra no meio menos denso, porém
decaindo de forma exponencial. Em geral, a profundidade de penetração
é da ordem do comprimento de onda da luz. Pictoricamente, é
como se houvesse uma rampa na qual uma partícula (fóton)
sobe um pouco mas depois volta. Este processo na óptica leva
o nome de penetração em barreira ou tunelamento fotônico.
Isto fica mais claro se colocarmos dois prismas próximos, separados
por uma distância da ordem do comprimento de onda da luz, como
representado na Fig. 6.17. Desprezando as reflexões de Fresnel
nas faces de entrada e saida dos prismas, vemos que a intensidade
da luz transmitida decai exponencialmente com a separação
entre os prismas, de acordo com IT
= I0 exp (-ad).
No interior de cada prima o campo elétrico oscila harmonicamente
na direção y, mas entre eles decai exponencialmente
como mostrado na Fig. 6.17.
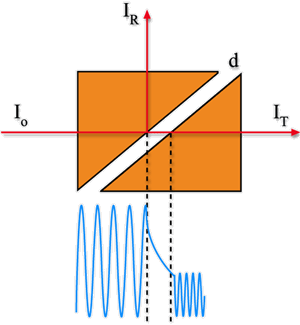
Fig. 6.17 - Tunelamento fotônico.
Este
é um fato muito importante, principalmente no que se refere
à propagação de luz em fibras óptica.
Nelas, o núcleo (com cerca de 5 mm de diâmetro) possui o índice de refração
levemente superior à da casca (diâmetro da ordem de 120
?m) e a tendência da luz é a de propagar confinada no
meio com maior índice de refração. Porém,
como acabamos de ver, uma parte não desprezível da radiação
propaga pela casca, devido ao tunelamento fotônico e qualquer
imperfeição (trincas, bolhas, etc.) acarreta em perdas
de intensidade.
Com
relação à energia transmitida ou refletida, podemos
escrever:
Chamando
de
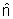 a normal à interface, a energia se propagando nesta direção
é
a normal à interface, a energia se propagando nesta direção
é
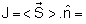
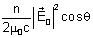 ,
a energia refletida é: ,
a energia refletida é:
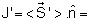
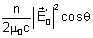 e a transmitida é dada por:
e a transmitida é dada por:

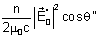 .
Define-se refletividade R e transmitividade T como: .
Define-se refletividade R e transmitividade T como:
onde
necessariamente T + R = 1.
Sergio Carlos Zilio
|