No caso da reflexão total interna, os coeficientes de reflexão para as polarizações s e p, podem ser escritos como e , onde as mudanças de fase e , que ocorrem durante a reflexão, são dadas por:

(6.38a)

(6.38b)

Se a onda incidente possuir as duas polarizações (s e p) haverá uma diferença de fase induzida pela reflexão total interna:

(6.39)

A Fig. 6.18 mostra a diferença de fase d como função do ângulo de incidência q para a reflexão total interna no vidro ( n₁ 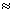1.5, n₁ = 1) cujo ângulo crítico é q_c = 41.9⁰. Vemos que próximo ao ângulo de 50⁰ , a

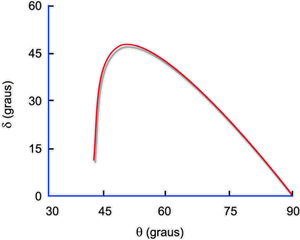
Fig. 6.18 - Diferença de fase como função do ângulo de incidência
para a reflexão total interna no vidro.

diferença de fase é 45⁰ e assim podemos pensar em obter luz circularmente polarizada, fazendo duas reflexões internas no vidro. Isto pode ser conseguido com o rombo de Fresnel, mostrado na Fig. 6.19 (a), tomando-se o cuidado de fazer as amplitudes dos campos com polarizações s e p iguais. Por outro lado, se provocarmos quatro reflexões internas, a diferença de fase induzida será de 180⁰ e como resultado teremos uma rotação no plano de polarização da luz linearmente polarizada incidente (Fig. 6.19 (b)). Neste caso, não é necessário fazer as polarizações s e p de mesma amplitude. A vantagem deste método de obtenção de luz circularmente polarizada e rotação do campo elétrico é a acromaticidade, isto é, a independência do comprimento de onda, ao contrário das lâminas l/4 e l/2.

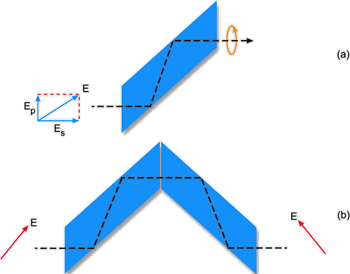
Fig. 6.19 - (a) obtenção de luz circularmente polarizada (rombo de Fresnel) e
(b) rotação do plano de polarização da luz.

Para finalizarmos esta seção, convém chamar a atenção para o fato de que o dispositivo da Fig. 6.19 (b) roda continuamente o plano de polarização da luz incidente, como é mostrado na Fig. 6.20. Este mesmo efeito ocorre para a lâmina de meia onda que estudamos na seção 6.4. Ao rodarmos o dispositivo (ou lâmina l/2), ou então mudando o plano de polarização da luz incidente de um ângulo q, a luz emergente sai com o plano de polarização rodado de 2q.

Sergio Carlos Zilio