Outro problema de interesse em física é aquele no qual uma partícula capaz de executar um movimento harmônico simples fica inserida num meio viscoso. Nesse meio surge uma força que tende a amortecer as oscilações. Imaginando uma força no meio proporcional à velocidade, escrevemos

.

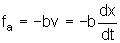Nessas circunstâncias a equação do oscilador amortecido é:

.

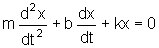A técnica para resolver equações diferenciais lineares como a equação anterior é procurar uma solução de forma

.

Claramente uma tal solução é uma função a valores complexos. As soluções fisicamente aceitáveis são a parte real ou imaginária de X(t). Isto é

x(t) = Re X(t).

ou

x(t) = ImX(t) .

Na realidade, tomamos uma superposição das duas.

Substituindo-se em 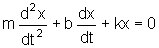encontramos

,

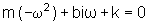cujas soluções são

.

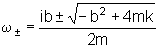Temos assim, três casos distintos, em função dos valores relativos de b² e 4mk :

a) b² > 4mk (oscilador superamortecido). A solução mais geral será

.

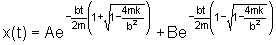b) b² = 4mk (oscilador criticamente amortecido). A solução será da forma

.

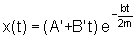c) b² < 4mk (oscilador sub-amortecido). A solução geral será da forma

.

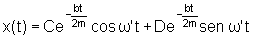onde

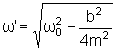Gil Marques