|
Consideremos
um oscilador harmônico simples sujeito a uma força externa
periódica da forma
.
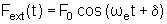A equação
do oscilador agora é
.
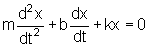A
solução geral da equação não homogênea
anterior é dada pela solução geral da equação
homogênea associada
mais uma solução particular de
,
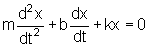isto é,
x(t)
= xh(t) + xp(t).
A
solução xh(t) foi determinada
no item anterior. Para determinar xp(t),
consideramos a equação auxiliar complexa
Se
xp(t) é uma solução
particular dessa equação, então
é
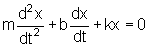uma solução particular de
.
Procuramos uma solução particular de
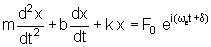na forma
,
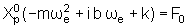
onde
x0 é uma constante a determinar.
Substituindo em
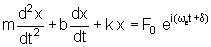obtemos
,
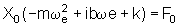e, portanto,
.
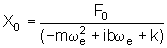Gil
Marques
|
