|
O movimento harmônico simples é definido como aquele
no qual a força que atua sobre a partícula tem a forma
|
A
lei de Newton
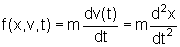então se escreve, nesse caso
 .
ou
seja, a força é proporcional ao deslocamento,
mas na direção contrária do mesmo. |
|
Um
exemplo simples desse tipo de força ocorre no caso em que procuramos
deformar uma substância elástica. Enquanto
a deformação não for muito grande a força
é proporcional ao deslocamento (ou à deformação
imposta), mas atua sempre no sentido contrário ao dele. É
uma tendência ou reação natural, no sentido de
buscar a restauração da forma original. Por isso k é
sempre referido como a constante elástica.
Podemos encontrar uma solução da equação
acima pelo método da tentativa e erro. Sabemos que a função
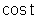é tal que
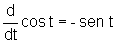
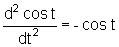
Portanto
a expressão acima nos sugere buscar uma solução
para
da forma
.
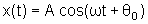Substituindo
em
constataremos que, de fato
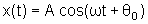é uma solução se
.
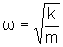
A
solução encontrada demonstra que o valor máximo
do deslocamento (xm) é
xm
= A .
A
é portanto a amplitude do movimento. A constante
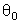é uma fase, por enquanto, arbitrária.
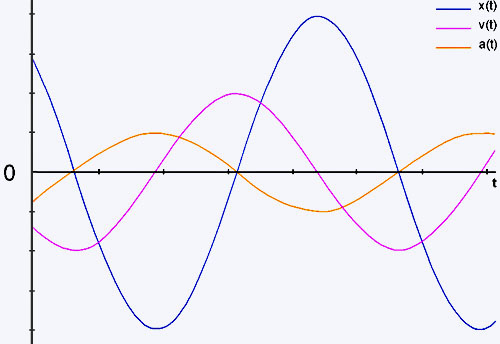
Note-se que o movimento nesse caso é periódico. O período
é determinado a partir da condição:
x(t
+ T) = x(t) .
De
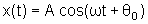segue que
Portanto, o período do movimento harmônico simples é
.
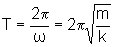A
freqüência, sendo o inverso do período será
dada por
.
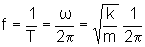As constantes A
e
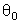podem ser determinadas a partir das condições iniciais.
Isto é, a partir da posição e da velocidade iniciais
Notemos
primeiramente que a velocidade da partícula no movimento
harmônico simples será dada por
.
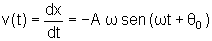
Portanto,
a velocidade máxima (ou mínima) da partícula
será dada pelo produto da amplitude pela freqüência
angular:
.
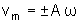A velocidade
máxima (ou mínima) ocorre nos pontos onde x = 0.
A aceleração será, de
.
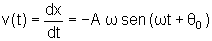
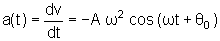
Como
esperado, obtemos de
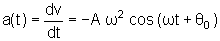e
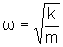que
.
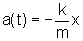Estamos
agora em condições de determinar a amplitude e a fase
em função de v0
e x0. De
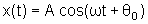segue que
.
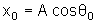De
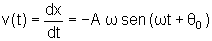segue que
.
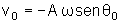Portanto,
a amplitude pode ser determinada, por exemplo, a partir das condições
iniciais. D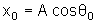e
e
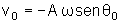segue que
.
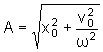e
.
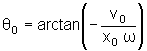Gil
Marques
|
