Queremos agora partir de luz linearmente polarizada e rodar seu plano de polarização ou gerar luz circularmente polarizada. Isto pode ser conseguido com um cristal anisotrópico cujo índice de refração depende da direção (birrefringência), como por exemplo, mica, quartzo, etc. Voltaremos a este tópico no capítulo que aborda a óptica de cristais. Considere a Fig. 6.6, onde luz linearmente polarizada incide sobre uma lâmina de espessura d com eixos rápido e lento respectivamente nas direções x e y.

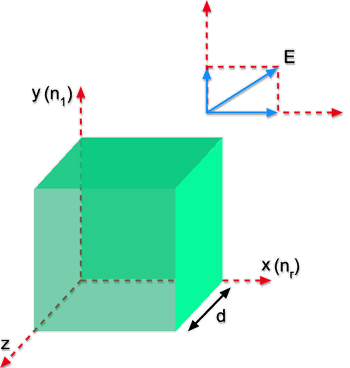
Fig. 6.6 - Incidência de luz sobre uma lâmina birrefringente.

O campo elétrico incidente forma um ângulo de 45° com o eixo x de maneira que suas componentes são: E_x = E₀ exp{i(k_rz-wt)} e Ey = E₀ exp{i(k_lz-wt)}. A onda atinge a placa em z = 0, onde E_x = E₀ exp{-iwt} e E_y = E₀ exp{-iwt}, e sai em z = d com: E_x(d) = E₀ exp{i(k_rd-wt)} e E_y(d) = E₀exp{i(k_ld-wt)}. A diferença de fase entre as componentes emergentes é:

(6.7)

Para termos luz circularmente polarizada, d = p/2 logo:

(6.8)

ou seja, a diferença de caminhos ópticos deve ser igual a um quarto de onda. Por outro lado, quando d=p, o plano de polarização da onda será rodado de 90°. Neste caso, a diferença de caminhos ópticos deve ser meia onda:

(6.9)

Se a luz incidente sobre a lâmina de meia onda não estiver com polarização a 45°, o campo será rodado por um ângulo 2q, como veremos na seção 6.7.

Sergio Carlos Zilio