No caso da polarização linear, a projeção do vetor 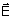sobre o plano xy descreve um segmento de reta. No entanto, quando (e consequentemente 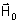) não for um número real, a projeção será uma elipse (ou circunferência, como veremos na próxima seção). Considere a soma de dois campos e 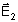, respectivamente nas direções x e y, conforme a Fig. 6.2. Ambos possuem a mesma frequência e vetor de onda, e são soluções possíveis da equação de ondas, que diferem por estarem rodados entre si de p/2. Além disto, eles podem também possuir uma diferença de fase relativa que chamaremos de d. As duas soluções são linearmente independentes e, como tal, combinações lineares delas fornecem outras soluções possíveis da equação de onda. Vejamos quais novos tipos de soluções podem advir destas combinações lineares.

Fig. 6.2 - Representação gráfica da orientação de duas soluções possíveis
para a equação de onda.

O campo resultante é dado por:

(6.2)

ou alternativamente, tomando a parte real:

(6.3)

A variação de 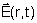no espaço e tempo está mostrada na Fig. 6.3 e sua projeção no plano xy, mostrada na Fig. 6.4, descreve uma elipse.

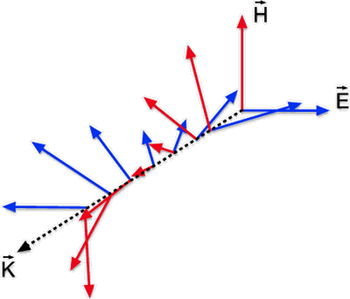
Fig. 6.3 - Onda plana com polarização elíptica.

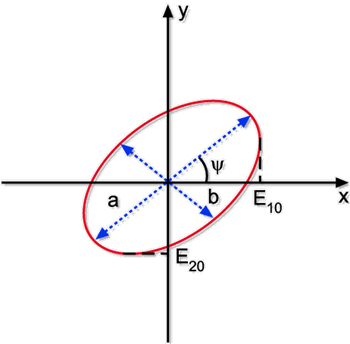
Fig. 6.4 - Projeção do campo elétrico no plano xy.

Esta elipse é descrita pelas equações:

(6.4a)

(6.4b)

(6.4c)

(6.4d)

cuja demonstração deixaremos como exercício. A elipse é caracterizada por a, b, e y, que são conhecidos como parâmetros de Stokes. Alguns casos particulares desta situação que estamos estudando ocorrem quando:

(6.5a)

(6.5b)

(6.5c)

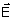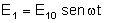Neste caso a projeção de no plano xy nos dá uma elipse que roda no sentido horário, tal que: e .
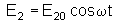Quando d = -p/2 teremos ainda uma elipse com os eixos principais, coincidindo com x e y mas com polarização no sentido anti-horário, como mostrado na Fig. 6.5d. De um modo geral, pode-se mostrar que para 0 < d < p temos polarização no sentido horário e para p < d < 2p no sentido anti-horário.

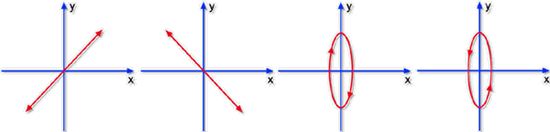
Fig. 6.5 - Alguns casos particulares de polarizações elípticas.

Sergio Carlos Zilio