À primeira vista pode parecer que se pode deduzir a primeira lei a partir da segunda. Na realidade, na ausência de forças, o movimento de uma partícula é uma trajetória retilínea e o movimento é uniforme e isso se pode deduzir da segunda lei.

O enunciado da primeira lei procura definir um conjunto de sistemas de referência ditos inerciais. Para qualquer um desses sistemas inerciais uma partícula, não estando sob a ação de forças, tem um movimento retilíneo e uniforme. Isso, como veremos depois, não é válido para sistemas não-inerciais.

Uma vez definidos os sistemas inerciais, podemos estabelecer, para esses sistemas, a relação entre força e aceleração (a segunda lei).

As equações de Newton podem ser escritas em coordenadas cartesianas, sob a forma mais geral como

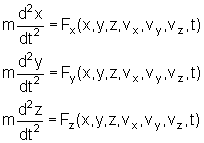
O problema central da mecânica se resume àquele de encontrar as soluções das equações de Newton. Trata-se de resolver, para o caso de se determinar a posição (x(t), y(t), z(t)) como função do tempo, um conjunto de equações diferenciais de segunda ordem no tempo. A dificuldade principal está no fato dessas equações estarem acopladas umas às outras.

A solução completa das equações de Newton requer que informações sobre a velocidade da partícula e sua posição sejam conhecidas em algum instante de tempo anterior ao tempo t.

Em geral admitimos que no instante de tempo t = 0 a posição e a velocidade da partícula são conhecidas

Assim, do ponto de vista matemático, o problema da mecânica se reduz a encontrar as soluções para as equações de Newton dadas as condições iniciais. Isto é, se forem conhecidas a velocidade e a posição da partícula no passado, podemos determiná-las no futuro, uma vez conhecidas as forças agindo sobre ela.

Gil Marques