|

Na seção
anterior tratamos o problema da coerência de dois campos chegando
ao mesmo ponto do espaço através de caminhos diferentes.
Queremos agora, discutir o problema mais geral de coerência
entre dois campos em diferentes pontos do espaço. Isto é
importante ao se estudar coerência de campos de radiação
produzidos por fontes extensas.
Considere a fonte pontual quase-monocromática da Fig. 8.7 e
os pontos de observação P1, P2
e P3 com campos E1, E2 e E3
respectivamente. Os pontos P1 e P3 estão
localizados na mesma direção da fonte, por isso entre
eles dizemos que existe uma coerência espacial longitudinal,
ao passo que entre P1 e P2, localizados à
mesma distância da fonte, a coerência espacial é
transversal.
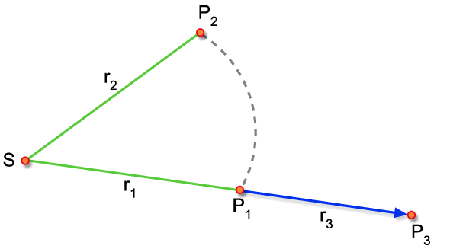
Fig. 8.7 - Fonte
pontual quase-monocromática.
É evidente que
a coerência longitudinal dependerá apenas de r13
= r3 – r1, ou equivalentemente, de t13
= r13/c. Para qualquer valor de E1(t), E3(t)
variará da mesma maneira, mas a um tempo t13 mais
tarde. Se t13 <<
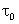 haverá uma alta coerência entre P1 e P3
enquanto que se t13 >>
haverá uma alta coerência entre P1 e P3
enquanto que se t13 >>
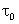 a coerência será pequena ou mesmo nula.
a coerência será pequena ou mesmo nula.
Já que uma fonte extensa pode ser considerada como composta
por uma infinidade de fontes pontuais independentes, é conveniente
estudar o caso de duas fontes pontuais isoladas. SA e SB
são fontes completamente incoerentes mostradas na Fig. 8.8.
Os campos elétrico nos pontos P1 e P2
são dados por:

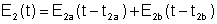
e a função de correlação normalizada entre
os campos E1 e E2 é:
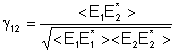
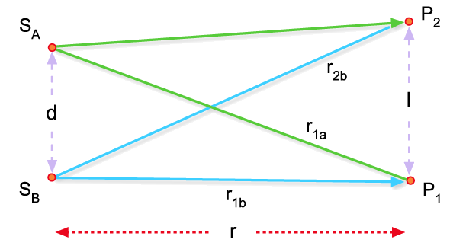
Fig. 8.8 - Fontes
pontuais completamente incoerentes.
Vamos chamar
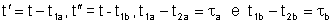 onde
onde
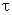 a
e a
e
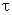 b
são os tempos de coerência transversal de SA
e SB. Logo, b
são os tempos de coerência transversal de SA
e SB. Logo,
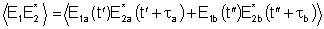
Note que na expressão acima não comparecem os termos
E1aE2b e E2aE2b, pois
as fontes são completamente incoerentes. Apenas os termos diretos
não são nulos, isto é,
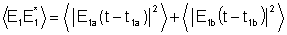
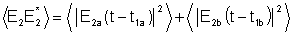
Como as fontes são equivalentes podemos escrever:
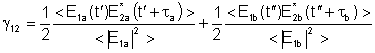
Logo,
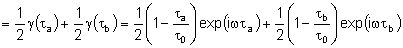
onde:

Se fizermos um esboço de
 como função da distância entre os pontos P1
e P2 teremos o gráfico da Fig. 8.9, onde os primeiros
mínimos saem da expressão:
como função da distância entre os pontos P1
e P2 teremos o gráfico da Fig. 8.9, onde os primeiros
mínimos saem da expressão:
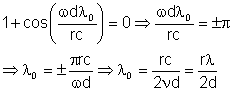
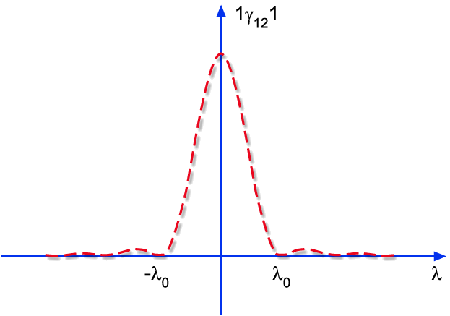
Fig. 8.9 - Correlação entre os campos 1 e 2.
Podemos chamar
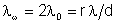 de comprimento de coerência transversal. Uma outra expressão
interessante pode ser derivada definindo
de comprimento de coerência transversal. Uma outra expressão
interessante pode ser derivada definindo
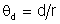 como na Fig. 8.10. Assim,
como na Fig. 8.10. Assim,
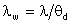 .
Esta expressão é muito importante para a medida de diâmetros
estelares através do experimento de dupla fenda. .
Esta expressão é muito importante para a medida de diâmetros
estelares através do experimento de dupla fenda.
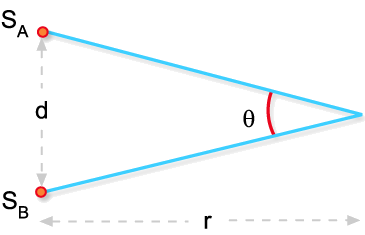
Fig. 8.10 - Definição
do ângulo de coerência.
Sergio Carlos Zilio
|