|

Atividade
óptica é a propriedade que certos materiais possuem
de rodar o plano de polarização de um feixe de luz linearmente
polarizada, da maneira indicada na Fig. 6.23. O ângulo de rotação
q do plano de polarização depende da distância
l percorrida pela luz dentro do meio e de uma característica
intrínseca do material, chamada de poder rotatório.
Costuma-se definir o poder rotatório específico como
sendo o ângulo rodado por unidade de comprimento. Olhando para
a direção z > 0, se a luz rodar para a direita o
material é chamado de destro-rotatório e se rodar para
a esquerda, levo-rotatório. Alguns exemplos de meios opticamente
ativos são: quartzo cristalino (com a luz se propagando na
direção do eixo óptico), clorato de sódio
e alguns tipos de açúcares. Na Fig. 6.24 vê-se
o poder rotatório do quartzo como função do comprimento
de onda. Notamos que esta grandeza varia com l
e esta variação, chamada de dispersão rotatória,
pode ser usada na determinação do comprimento de onda
de luz monocromática, ou como monocromador por atividade óptica,
colocando-se um polarizador na entrada do meio e um analisador na
saída deste. Variando-se o ângulo do analisador podemos
alterar o comprimento de onda que sai do monocromador.
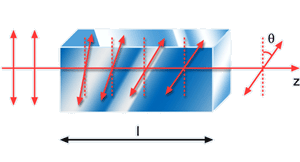
Fig. 6.23 - Rotação do plano de polarização
da luz devido à
atividade
óptica do meio.
A
atividade óptica pode ser explicada levando-se em conta a simetria
do meio. De acordo com a Fig. 6.25, quando a luz linearmente polarizada
incide sobre o material, as componentes x e y estarão sujeitas
a mesma simetria e portanto possuem a mesma velocidade de propagação
(mesmo índice de refração). Já no caso
de luz circularmente polarizada, as componentes polarizadas à
direita (s+) e à esquerda
(s-) "encontram" os triângulos
de formas diferentes e portanto "vêem" simetrias diferentes.
Isto faz com que os índices de refração n+
e n- para estas duas polarizações sejam diferentes
e como consequência, estas polarizações adquirem
fases diferentes durante sua propagação pela amostra.
Este fato pode ser melhor apreciado se usarmos o formalismo matricial
de Jones.
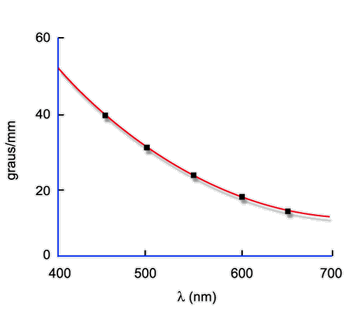
Fig. 6.24 - Poder rotatório específico do quartzo cristalino
como função
do comprimento de onda.
Consideremos
um feixe de luz linearmente polarizada na direção x,
propagando-se ao longo do eixo z. Podemos decompor esta luz em duas
componentes circularmente polarizadas, ortogonais. No formalismo de
Jones, este fato se expressa como:
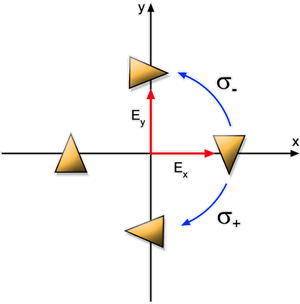
Fig. 6.25 - Explicação da atividade óptica baseada
na simetria do meio.
Após
percorrer uma distância l dentro do meio, as componentes s+ e s-
adquirem fases diferentes e o campo elétrico na saída
da amostra pode ser escrito da forma:
onde
foram introduzidas as quantidades
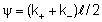 e e
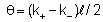 .
Somando as matrizes obtemos: .
Somando as matrizes obtemos:
que
representa uma onda linearmente polarizada, cuja direção
do plano de polarização encontra-se rodado de um ângulo
com relação a direção inicial (antes da
luz penetrar no meio). De acordo com a definição de
temos:
de
forma que o poder rotatório específico é dado
por:
Sergio Carlos Zilio
|