EXPRESSÕES PARA VELOCIDADE E A ACELERAÇÃO NO MOVIMENTO HARMÔNICO SIMPLES

Pode-se mostrar que num movimento harmônico simples, a velocidade da partícula em função do tempo, e para x dado pela expressão , é dada por

,

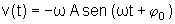onde as constantes A, 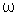e 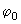são aquelas definidas anteriormente.

A aceleração varia, igualmente com o tempo. Sua variação é análoga àquela da posição:

,

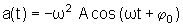onde, de novo, aqui se aplicam as definições de A, 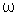e 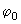já dadas.

Observe-se de 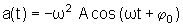e x(t) = A cos(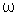t + 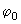) que podemos tirar uma relação entre a aceleração e a posição de uma partícula a qual é:

.

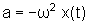Essa relação decorre de uma propriedade geral do movimento harmônico simples. De fato, essa propriedade é uma forma de definir o MHS.

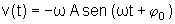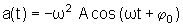Observando as expressões e notamos que os valores máximos para a velocidade e aceleração são

.

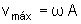
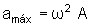Na figura abaixo apresentamos os gráficos de x x t, v x t e a x t e do movimento harmônico simples.

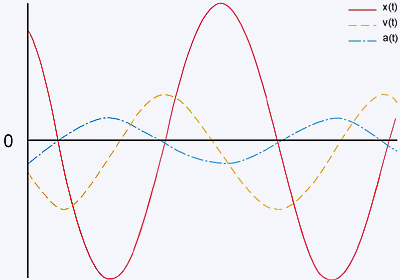
Observe-se quando o móvel atinge os valores máximo (x = +A) e mínimo (x = -A) a velocidade do móvel é nula. Nos pontos de maior velocidade (em qualquer direção), o valor de x (e o da aceleração) é igual a zero.