Como já foi visto anteriormente, para uma partícula de massa m constante e velocidade , em cada instante o vetor quantidade de movimento tem um módulo, uma direção e um sentido, conforme a equação

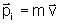
A variação temporal da quantidade de movimento , quando 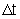é um intervalo muito pequeno, costuma ser representada por 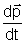. Tant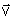o como 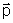, a velocidade e a quantidade de movimento são grandezas vetoriais, de movo que a relação vale um módulo, direção e sentido. A massa de uma partícula é suposta constante e é uma grandeza escalar. Se a massa é constante, uma variação temporal 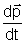só pode ser devida à variação temporal da velocidade

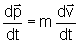
Mas uma variação temporal da velocidade é a aceleração; então,

é assim uma outra forma de representar a lei de Newton.

Na Física, estamos sempre lidando com um sistema muito grande de partículas. Primeiramente, vamos estudar o sistema mais simples de todos, composto por apenas duas partículas.

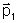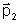Consideremos duas partículas, cujas quantidades de movimento são e . Podemos, portanto, escrever, usando a Lei de Newton:

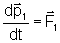
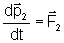
Sobre as partículas atuam dois tipos de forças: forças externas e forças internas (forças exercidas por uma partícula sobre a outra). Se somarmos as duas equações, as forças internas se cancelam, pois uma é a reação da outra. Somando as duas equações teremos:

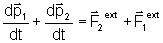
Pode-se mostrar que:

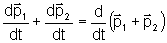
Assim, definindo a quantidade de movimento total (p) por

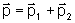
concluímos que

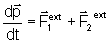
Se não houver forças externas teremos

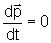
Ora, se a taxa de variação de uma grandeza com o tempo for nula, isto significa que essa grandeza é constante no tempo.

Concluímos pois que, na ausência de força externa, a quantidade de movimento é constante.

Suponha o choque entre duas bolinhas de gude. Uma bolinha fica parada numa concavidade do solo e uma outra é arremessada sobre ela. No momento do arremesso está sendo aplicada uma força. Mas, logo depois, não há nenhuma força se o atrito com o solo for desprezado, o que é razoável de se supor. Então, teremos duas bolinhas, uma em movimento e outra parada, logo depois do arremesso, sem nenhuma força agindo sobre elas. Logo depois de ocorrer o choque, as duas bolinhas serão arremessadas em direções tais que haja conservação da quantidade de movimento, sem nenhuma força aplicada ao sistema logo antes e logo depois de ocorrer o choque.

Note que supusemos que não há força de atrito entre o solo e a bolinha. No momento do arremesso, a força aplicada é muito maior que a força de atrito, que tenderia a frear a bolinha. Se, entretanto, realmente não houver atrito algum, as bolinhas iriam até o infinito! Por isso, analisamos o problema apenas em instantes logo antes e logo depois do choque.

Marques e Ueta