
Calculemos
as forças que, reciprocamente, se exercem dois condutores
retilíneos, paralelos, afastados pela distância a (fig. 295).
Seja
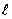 o comprimento dos condutores, i1
a corrente do condutor (1), i2 a do
condutor (2). Calculemos a força que o condutor
(1) exerce sobre o condutor (2).
o comprimento dos condutores, i1
a corrente do condutor (1), i2 a do
condutor (2). Calculemos a força que o condutor
(1) exerce sobre o condutor (2).
O
condutor (1) produz, em todos os pontos do condutor (2)
um campo cuja indução magnética tem:
módulo:
dado pela lei de Biot e Savart
|
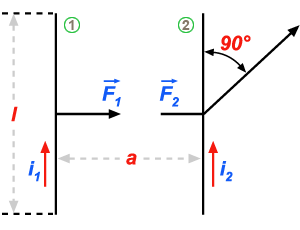 Figura 295 Figura 295 |
direção:
perpendicular ao plano dos dois condutores.
sentido:
para trás da figura (verifique pela regra do boneco, de Ampère).
Em todos
os pontos do condutor (2) existe uma indução igual a essa
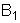 . Então tudo se passa como se o condutor (2) estivesse
em um campo magnético uniforme de indução magnética
. Então tudo se passa como se o condutor (2) estivesse
em um campo magnético uniforme de indução magnética
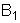 e perpendicular ao condutor. A força
e perpendicular ao condutor. A força
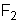 que atua nesse condutor tem então:
que atua nesse condutor tem então:
direção:
perpendicular ao plano determinado por
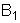 e o condutor, portanto, está no plano da figura.
e o condutor, portanto, está no plano da figura.
sentido:
do condutor (2) para o condutor (1) (verificar pela
regra dos três dedos da mão esquerda).
módulo:
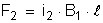 (tópico "Cálculo
da Força - 2a. lei elementar de Laplace",
1o caso particular).
(tópico "Cálculo
da Força - 2a. lei elementar de Laplace",
1o caso particular).
Substituindo
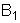 pelo seu valor, resulta:
pelo seu valor, resulta:
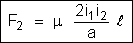
Essa é a
importantíssima fórmula tomada como base para a definição do
AMPÈRE, à qual já nos referimos nos tópicos "A
Formação do Sistema MKS em Eletricidade"
e "Sistemas
de Unidades em Magnetismo e Eletromagnetismo" .
Deixamos
a cargo do leitor demonstrar o seguinte:
1o) que
a força
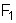 que o condutor (2) exerce sobre o condutor (1)
tem êsse mesmo valor, e é dirigida para o condutor (2);
que o condutor (2) exerce sobre o condutor (1)
tem êsse mesmo valor, e é dirigida para o condutor (2);
2o) vemos
que, no caso da figura acima, em que as duas correntes
têm o mesmo sentido, os dois condutores se atraem; demonstre
que quando as duas correntes têm sentidos opostos os condutores
se repelem.