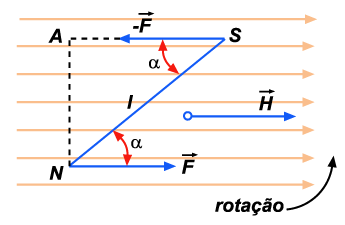|
 Figura 243 |
A força que
atua na massa magnética sul tem igual módulo (por isso a representamos
por
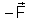). As forças
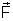e
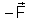tendo igual módulo, mesma direção e sentido opostos, formam
um binário. Esse binário tende a fazer o ímã entrar em rotação
no sentido indicado na figura acima.
Sabemos, da
Mecânica, que o momento de um binário é igual ao produto do módulo
de uma das forças pela distância entre as forças.
Representando
por C a esse momento, temos:
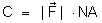
Sendo
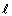o comprimento do ímã e
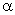o ângulo que o eixo do ímã faz com a direção do campo, temos:
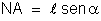
Fica:
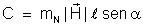
Mas,
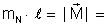módulo do momento magnético do ímã. Resulta:
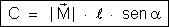
Esse
conjugado imprime ao ímã um movimento de rotação, até que
o ímã tome uma posição na qual o ângulo
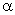se anula. Nessa posição,
, e o conjugado se anula (fig. 244). Mas,
o ímã não pára bruscamente, por causa da inércia; atingindo
a posição indicada na figura 244 ele continua o
seu movimento, passando além da posição de equilíbrio.
Mas, quando passa dessa posição, o conjugado atua em sentido
oposto e faz o ímã voltar (fig. 245). Isso acontece
diversas vezes, isto é, o ímã entra em oscilação, e depois
pára com o seu eixo na direção do campo. É isso o que acontece
com a bússola; ela oscila várias vezes e depois pára com
o eixo na direção do campo magnético terrestre, pois este,
em pequena extensão, pode ser considerado uniforme.
|
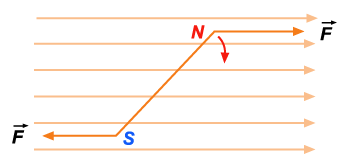 Figura 244 |
Figura 245
Suponhamos um
pólo plano com densidade magnética
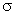e um ponto A infinitamente próximo desse polo. O cálculo
do campo magnético nesse ponto A é idêntico ao cálculo do campo
elétrico num ponto próximo de um plano uniformemente eletrizado
(veja o tópico "Campo
Elétrico em um Ponto Próximo de um Plano"
). Chegamos à seguinte conclusão:
Vale:
Perpendicular
ao polo.
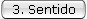
Do polo para
o ponto A se for polo norte; do ponto A para o polo, se for polo
sul (fig. 246).
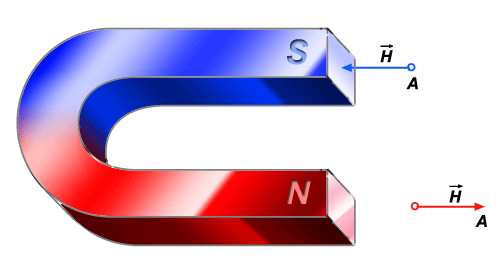
Figura 246
É muito importante
para nós o caso em que um polo plano norte é situado infinitamente
próximo e paralelo a um polo plano sul, e com suas densidades magnéticas
de mesmo valor absoluto:
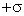no polo sul (fig. 247). Considerando-se um ponto A entre os dois planos,
se existisse só o polo norte ele produziria em A um campo magnético
de módulo
,
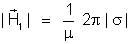perpendicular
aos polos e dirigido do polo norte para o polo sul. Se existisse
só o polo sul, ele produziria em A um campo magnético de valor absoluto
igual a esse
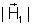, também perpendicular aos polos e dirigido do polo norte
para o polo sul. Então os dois polos produzem em A campos iguais.
O campo resultante em A será o dobro de
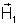, isto é, será perpendicular aos polos, será dirigido do
polo norte para o polo sul, e terá por módulo:
ou
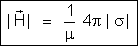
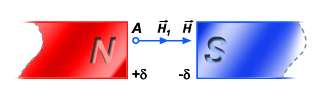
Figura 247
É importante
notar que nas fórmulas
e
,
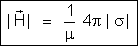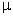é a permeabilidade magnética do meio em que se produz o
campo magnético.
Já provamos,
no tópico "Relação
entre |I| e ||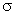
em um imã de forma de prisma reto" ,
que o valor absoluto da densidade magnética dos polos do ímã é igual
ao módulo de intensidade de imantação. Então, sendo
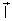a intensidade de imantação do ímã que produz o campo no
ponto A, as fórmulas
e
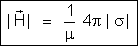podem ser escritas, respectivamente:
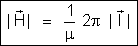e
. A massa magnética norte do ímã fica sujeita a
uma força
. 
