
Seja
o campo produzido pela massa magnética M. Suponhamos que
num ponto A desse campo seja colocada a massa magnética puntiforme
m, suficientemente pequena para não alterar o campo magnético
de M (fig. 235). Em m atuará uma força
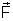 , que pode ser de atração ou repulsão, de acordo com
os sinais de M e m. Suponhamos que retiremos do ponto A a
massa magnética m e coloquemos nesse mesmo ponto, sucessivamente,
as massas magnéticas
, que pode ser de atração ou repulsão, de acordo com
os sinais de M e m. Suponhamos que retiremos do ponto A a
massa magnética m e coloquemos nesse mesmo ponto, sucessivamente,
as massas magnéticas
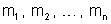 , todas elas satisfazendo as duas condições: puntiformes,
e suficientemente pequenas para não alterarem o campo de M.
Nessas massas atuarão, respectivamente, as forças
, todas elas satisfazendo as duas condições: puntiformes,
e suficientemente pequenas para não alterarem o campo de M.
Nessas massas atuarão, respectivamente, as forças
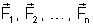 . A propriedade fundamental do campo magnético é a
seguinte: o quociente dessas forças pelas massas magnéticas
correspondentes colocadas em A é uma grandeza vetorial constante
em módulo, direção e sentido, para o mesmo ponto A
. A propriedade fundamental do campo magnético é a
seguinte: o quociente dessas forças pelas massas magnéticas
correspondentes colocadas em A é uma grandeza vetorial constante
em módulo, direção e sentido, para o mesmo ponto A |
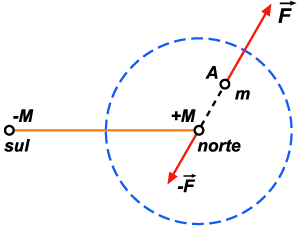 Figura 235 Figura 235 |
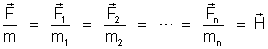 (constante)
(constante)
Essa grandeza
vetorial
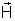 é chamada vetor campo magnético, ou simplesmente, o campo
magnético no ponto A. Considerando só uma igualdade, temos:
é chamada vetor campo magnético, ou simplesmente, o campo
magnético no ponto A. Considerando só uma igualdade, temos:
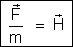 ou
ou
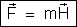
A equação
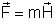 do campo magnético é a que corresponde à equação
do campo magnético é a que corresponde à equação
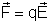 do campo elétrico, e
do campo elétrico, e
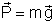 do campo gravitacional (veja o tópico
"Propriedade
Fundamental do Campo Elétrico" ).
do campo gravitacional (veja o tópico
"Propriedade
Fundamental do Campo Elétrico" ).
Considerando
os módulos de
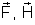 e m, temos:
e m, temos:
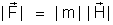
Quando
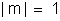 , resulta
, resulta
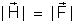
Significa que
o módulo do campo magnético em um ponto é igual à intensidade da
força que atua sobre a unidade de massa magnética colocada nesse
ponto.
A equação
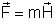 mostra que a força que atua na massa magnética m colocada
em um campo magnético depende de dois fatores:
mostra que a força que atua na massa magnética m colocada
em um campo magnético depende de dois fatores:
1o) da própria massa m;
2o) do fator vetorial
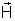 , que não depende de m, mas sim do ponto em que ela é colocada.
, que não depende de m, mas sim do ponto em que ela é colocada.
Recorde o tópico
"Propriedade
Fundamental do Campo Elétrico" .